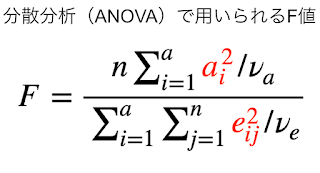Home Posts filed under 統計
ラベル 統計 の投稿を表示しています。 すべての投稿を表示
ラベル 統計 の投稿を表示しています。 すべての投稿を表示

2020/06/21

分散分析(ANOVA)の理解を深めるために

医療統計で使われる分散分析（ANOVA）について


医療統計でよく出てくる統計手法に分散分析があります。分散分析の英語での名称はANalysis Of VArianceです。 大文字部分をとってANOVAとも呼ばれます。

例えば、降圧剤の試験で、薬の種類や投与量を変えて血圧値を測り、効果を見たい場合などに使われます。プラセボと薬A、薬Bなど薬の種類のみを変える時、データの値を変化させる原因（変数）は１つとなります。このような分散分析を一元配置分散分析（one-way ANOVA)といいます。薬の種類と投与量を同時に変化させる場合は、二元配置分散分析と言います。 一元分散分析も二元分散分析も考え方は分散分析として同じです。


分散分析の考え方


分散分析の利点は、多群の比較ができることです。t検定では２群までしか比較できませんが、分散分析では、３群以上の比較に用いられます。上記の例だと薬の種類を複数種類（３種類以上）一度に検定できます。2群の場合はt検定でも結果が同じになるので、通常は用いられません（わざわざ使う必要がありません）。t検定の多群への拡張が分散分析と考えることもできます。

t検定が平均値と標準誤差から説明できることを下記の著書により説明しましたが、分散分析も同様の考え方で、有意差を説明できます。


医療統計入門 iBooks版（購入はこちら）
医療統計入門 Kindle版（購入はこちら） 


分散分析法のネーミングが直感的な理解を妨げているように思います。これは歴史的な経緯もあります。1918年に『The Correlation Between Relatives on the Supposition of Mendelian Inheritance（メンデル遺伝の仮定における親族間の相関関係）』という論文で、ロナルド・フィッシャー(Ronald Fisher)が「分散」という用語（概念）を使ったのが始まりです。その後、1925年にフィッシャーが『Statistical Methods for Research Workers（研究者のための統計学的方法）』に分散分析法を載せたことで、広く知られるようになりました。最初に分散（の概念を用いること）に気がついて「分散」分析と言ってしまったのですが、分散を分析するのではありません。分散を用いて、多群の平均値とバラツキを分析する手法が分散分析法になります。

分散分析は、「2つ以上の群の中の標本が同じ平均値を持つ母集団から取られた」という帰無仮説を検定」するための方法であり、具体的にどの群とどの群の間に差があったかを知るためには、多重比較を行う必要があります。
もう少し口語的に書き直すと、検定の結果「薬の種類を変えたとしても降圧効果に差がなかった」とはどうも言えない場合（きっと何か差がある！有意差あり）でも、どの薬のために結果が変わったのかは分からない、となります。


分散分析における数式の見方


「医療統計入門」では、数式を使用せずに説明をしましたが、こちらでは少し数式を扱いたいと思います。


医療統計入門 iBooks版（購入はこちら）
医療統計入門 Kindle版（購入はこちら） 


話がややこしくなるので、プラセボ、薬A、薬Bの３群（a=3）を比較をする一元配置分散分析で、かつ、理想的な場合を想定して、各群の試験回数はn回で共通とします。（途中でデータが取れなかったりすることがなく、綺麗なデータが取れたとします。）

その時にF値は下記のように表せます。


分散分析のF値（F-value in ANOVA）


分散分析では、効果（によって説明される平均平方）を分子、誤差（によって説明される平均平方）を分母とすることでF値を計算します（F検定）。

具体的に見ていきます。統計においては、数値の大きさを比較したい場合に、符号の絶対値ではなく、２乗することがあります。


|-1| < |2| < |-3| (絶対値の大小)
（−１）2 ＝１
　　22　＝4
（−3）2 ＝9
　1 < 4 < 9 (2乗の大小)　


Σは和を取るということなので、aiとeijが何を示しているのかが分かれば、分散分析の数式で何が比較されているかを理解できたことになります。

結論を言うと、aiとは全部の群の平均値から各群までの平均値の差になります。 eijは各群の平均値から試験された個別のデータまでの差になります。 言葉で説明されるより図を見ていただいた方が理解しやすいと思います。


分散分析（ANOVA）

νaは自由度（群間）、νeは自由度（残差）になります。自由度は群数や試験回数（データ数）で表される補正値になります。


νa = 群数(a)-1
νe = 群数(a)×（試験回数(n)−１）


具体的にデータがどのような平均値、バラツキを持った時に有意差が出るのかについては、著書の方で説明しておりますので、ご参照ください。


iBooksバージョン（Apple Books）




Kindleバージョン（Amazon）


(関連コンテンツ) 
医療統計学が難しい理由
現場で役立つ医療統計スキル習得のための最短経路
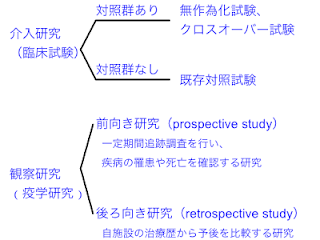
臨床論文に出てくる試験デザインの分類と種類
文献によく出てくるt検定の種類、3つ。
検定の多重性について
標準偏差が分かるための正規分布。確率分布を理解して疑問を解決。
サブグループ解析でのハザード比（HR）の読み方
カプランマイヤーなどの生存時間解析で試験の背景比較がよくない訳
どれをインストールしたらいい？医療で使える統計解析ソフトウェア６選
電子書籍「医療統計入門　〜統計の基礎からt検定、 分散分析(ANOVA)まで〜」（iBooks/Kindle）

2020/06/06

医療統計から考えるアビガンのマーケティング戦略（新型コロナウイルス）（2020/6/6）

2020年6月6日の情報に基づき記事を作成しています。
内容については、最新の情報をご確認上ご判断ください。

photo by NIAID

新型コロナウイルスに対する医薬品の適応拡大


アビガンの臨床試験について、医療統計と医療マーケティングの立場から考察してみたいと思います。今、新型コロナウイルスに対する医薬品として注目されているものは、適応拡大であり、既存治療の中で使われてきたものです。適応拡大とは、他の疾患での治療に使われていた薬を別の疾患に使うことをいいます。

5月７日にレムでシビルが特例承認されるまで、新型コロナウイルスに有効な薬がない状態でした。 ベクルリー（レムデシビル：Remdesivir）はエボラウイルス感染症に対する治療薬として開発された薬剤です。アビガン（ファビピラビル：favilavir）も抗インフルエンザ薬として開発された薬剤です。

未知の副作用が起こる可能性は否定できません。ただし、適応拡大の利点は、ある程度、安全性が似たものになることです。例えば、全く警戒していないところで催奇形性が起こるのではなく、アビガンでは既に催奇形性が知られていることがあります。 （例えば、オブジーボなどの抗癌剤でも、悪性黒色腫から始まり現在９種類のガンに使用されています。腫瘍という共通の土台の上で、経験値が活かせる可能性があります。）

新型コロナウイルスの重症度と治療の選択肢


新型コロナウイルスの治療では、呼吸器を主たる目安として重症度が分類されています。厳密ではないかもしれませんが、ウイルスの増殖による臓器への負担が体調を悪化させる軽症から中等症とサイトカインストームにより免疫が暴走による重症に分けられます。

軽症から中等症の治療を考えるときに、新型コロナウイルスの増殖抑制があります。 レムデシビルもアビガンも体内でRNAの元となる物質（リボ核酸）に似たものとなります。新型コロナウイルスはRNAウイルスでウイルスが増えるためには、RNAをコピーする過程が必要になります。このコピーの際に、これらの物質が材料（リボ核酸）として誤って取り込まれ、新型コロナウイルスのRNAが伸びるのをストップさせます。その結果、増殖を抑止します。これが、レムデシビルとアビガンの作用の仕方です。


武漢ウイルス研究所が新型コロナウイルスに対する培養細胞（Vero E6：アフリカミドリザル腎由来）の実験で効果を検討しています。


違いはベクルリー（レムデシビル）は注射薬ですが、アビガン（ファビピラビル）は飲み薬（経口）です。ベクルリー（レムデシビル）は中等症から重症患者を対象としています。おそらくこの投与経路の違いがレムデシビルとアビガンの開発戦略の違いを生み出しているのだと思います。

アビガンの検証的な臨床試験


原則として、医薬品の有効性は、臨床試験により、統計的な有意差が検証されることが必要です。観察研究は、薬の真の効きや安全性を担保すると言うよりも、医薬品に対する新たな知見を付与することが、その第一義的役割です。観察研究における症例の集積により、医薬品の効果の検証ができるものではありません。

アビガンに関しては、様々な臨床試験が動いています。今回着目するのは、試験実施者が富士フイルム富山化学株式会社の「非重篤な肺炎を有するCOVID-19患者を対象としたファビピラビルの有効性及び安全性の検討−アダプティブ、単盲検、ランダム化、多施設共同比較試験-（非重篤な肺炎を有するCOVID-19患者を対象としたファビピラビルの臨床第3相試験）」です。 医薬品としての担保と言う意味では、「ファビピラビルの臨床第3相試験」が適切だと思います。

アビガンの臨床第3相試験の対象者は非重篤な肺炎を有するCOVID-19患者


試験概要を見ると対象者は非重篤な肺炎を有するCOVID-19患者です。 医療マーケティングの視点からこのデザインを眺めると、ファーストライン（第一選択薬）を狙う戦略に見えます。治療を大きく軽症、中等症、重症に分けるのであれば、治療初期に使われる方が、患者数（パイ）が大きくなります。

新型コロナウイルスの話ではないですが、例えば、抗癌剤での薬剤選択を見てみます。抗癌剤では、作用の仕組みが同じような薬剤が複数選択できるような状況では、どの薬を使うか、どの順番に使うかが問題になります。最初に使われる薬の方が当然ながら患者数（パイ）が大きく、製薬企業も第一選択薬として使われることを望みます。ただ、医薬品の開発の観点から見ると、既存治療のあるものは、医薬品の誕生とともに第一選択薬になることはあまりありません。最初は少数例でそして徐々に臨床試験や使用実績を積み重ねて、選択の順位（ライン）を上げていく、薬を育てていくことが行われます。
まずは治療薬として採用され、他の可能性のある薬が出てきたときには、併用を順次試していく。レムデシビルでは、この戦略に沿っているように思います。

話は戻って、もし、今後アビガンが承認されることがあれば、治療ではレムデシビルより前に使われることになります。しかも軽症例で使われることになります。既存の治療がないので、第一選択薬を狙うと言うのは、戦略としてあり得るのかもしれません。ここから後は経済とか国家間の取引の話になるのかも知れません。ただ、飲み薬（経口）というのもあるのかもしれませんが、負うべきリスクも大きくなるように思います。

予定試験期間が3月31日～6月30日までなので、解析も合わせて、その後どのような結果になるのか興味のあるところです。今一度、有事だからエビデンスが不十分でも良いとなれば、ウイルスと闘う医療従事者の武器が何なのか分からなくなってしまいます。理論的に治療ができる、きちんとしたエビデンスが欲しいというのが率直な感想になります。また試験の途中はバイアスがかからないように、慎重に見守っていく必要があると思います。

その他、新型コロナウイルスの治療薬として候補に挙がっている医薬品は下記のものがあります。


2019/03/28

臨床論文に出てくる試験デザインの分類と種類

はじめに

医療系の論文・文献には○○試験というものが何種類も出てくる。ざっと挙げただけで試験という名の付くものは下記のようなものがある。特にこういった文献を読み始めた初学の時には混乱しがちである。
  • 無作為化試験
  • クロスオーバー試験
  • 既存対照試験
  • 優越性試験
  • 非劣性試験
ではどうすればいいかというと、時間軸や介入の有無で試験デザインを分類すると分かりやすい。 時間軸は前向き研究（prospective study）や後ろ向き研究（retrospective study）と言われるもので縦断研究と言われる。横断研究はある時点での状況を表したものになる。

介入試験

もう一つの介入とは一般には使わない言葉だが、辞書には自然ではない管理した状態を表すとある。英語ではInterventionだ。介入の対義語は傍観であるが、ありのままということになる。なので、介入とは「ありのままでない」ということで、人為的に試験の環境を整えて、試験結果を精密にしようとする試みを言っている。言い換えれば、介入研究の目的は既知・未知の交絡因子の影響を最小限にとどめるようにすることだとも言える。交絡因子とは因果関係に間接的に影響を与える条件のことをいう。

この介入研究には比較する群、対照群（コントロール群）があるかないかによって更に細分化される。対照群がある場合の例としては、無作為化試験、クロスオーバー試験がある。他方、単群での介入試験としてはhistorical controlと呼ばれる既存対照試験がある。介入研究は何かしらの試験環境を整えてからある程度予想できたとしても未知な結果を導き出す所作であると考えれば、全て前向きであることが分かる。

優越試験と非劣性試験

もう一つ、優越性試験、非劣性試験は介入試験の判定をどのように行うかで分類したもの。優越性試験ではいずれかの群が他の群より有意に優れているかを検証する。非劣性試験では、ある範囲であれば同じだろうと思われる範囲、非劣性マージンを設けて、そのマージンよりも劣らないということを証明する。優越性試験だけではどちらの薬がいいか悪いのかだけの結論になってしまうが、実際には効果が似たようなものであれば、副作用が少ないものの方がいいこともある。これが非劣性試験が行われる主な理由になっている。

観察研究

介入研究に対して観察研究がある。何らかの手を加えて理想的な試験状態を作らない、ありのままがどうなっているのかを知るための研究だ。観察研究では対照群がない場合は記述研究、ある場合は分析研究となる。コホートという言葉が出てきたら疫学における観察研究になるので、検証的な臨床試験ということはない。ちなみに、コホートとは「共通点があり、観察の対象とする集団」のことをいう。例えば、健康な人の集団で、血圧や栄養状態を調査し，その後一定期間追跡調査を行い，疾病の罹患や死亡を確認するような研究をいう。ある時点から将来に渡って調べているので、前向き研究（prospective study）になる。後ろ向き研究（retrospective study）としてはケースコントロール研究があり、自施設の治療歴から予後を比較するような研究をいう。



まとめ

なぜこんなことを書いたかというと、文献の検索をしているとどういう目的で文献が書かれているかを見失うことがあるからだ。いわゆる観察研究なのに検証結果を探してしまったり、介入試験の患者背景を疫学として扱ったりすることだ。文献がどの分類に当たることを報告しているか見当をつけることで少しだけ労力が減ることを願っている。

2018/08/17

有意水準と確率値の違い。過誤の種類とP値の読み方

有意水準と確率値の関係

第3相試験のように検証的な試験では、P値には2つの可能性があります。 1つは有意水準でもう１つが臨床試験のデータから計算された確率値（P値）です。
検証的試験は何度試験をしても同じ結果が得られることを期待して設計されます。 例数設計などの手段を使っています。 「P=・・・」と書かれた場合はある例数の時に計算されたP値（確率値）です。 繰り返し同じ試験をすることが可能な場合はこの確率値は毎回少しずつ違うものになるでしょう。 P<0.05などの有意水準は判定値を示します。上手く試験が行われた場合に試験の確からしさを有意差として示します。（帰無仮説の棄却）

２通りの試験結果が外れるパターン

仮に試験を複数回行うとまぐれで有意水準を満たすことがあります。 本当は間違っているのに正しいと判断してしまうことを第１種の過誤と言います。 逆に本当は正しいのに間違っていると判断することを第２種の過誤と言います。 結果が外れるパターンにはこのように第１種の過誤（Type Ⅰ error：偽陽性False positive、αエラー ）と第２種の過誤（Type Ⅱ error：偽陰性False negative、βエラー ）の２通りがあります。 第１種の過誤は「あわてん坊のエラー」、第２種の過誤は「ぼんやり者（見過ごし）のエラー」とも言われます。
過誤の表現に対する別表現
  • 第１種の過誤（Type Ⅰ error）
    偽陽性False positive、αエラー　→ 「あわてん坊のエラー」
  • 第２種の過誤（Type Ⅱ error）
    偽陰性False negative、βエラー → 「ぼんやり者（見過ごし）のエラー」

過誤を考慮した有意水準の設定

一般的に有意水準を表すP値は第1種の過誤の判定値（α）を表します。 第１種でも 第２種でも過誤の確率は小さいに越したことはありませんが、両方の過誤を同時に小さくすることはできません。そのためα<0.05など過誤の水準を一定値まで認めるということで試験デザインに記載されます。これがP<0.05となります。 不等号で書かれたP値が常に有意水準を表すかというと、確率値の小数点以下で有効桁数よりも小さい場合に「P<0.00…」と書かれることがあります。試験が複数回行われると確率値が異なることから考えると、確率値が小さいからといってそれが有意差の大きさを示さないこともわかると思います。
時々医療用医薬品を説明する資材で有意水準を表しているのか、実データからの値を示しているのか分からないものがあります。資材を読む際や説明をしたり、されたりする際には一度確認してみるといいかもしれません。

まとめ

試験に差があるかどうか、誤まって差があるとしたり 、見過ごされるかのバランスを考える必要があります。これを過誤として説明しました。１回の試験で見出された確率値とこの過誤のバランスから判断される有意水準の違いを説明しました。 

下記の電子書籍では有意水準の説明をグラフを用いて説明しています。パラパラと読めるようにしたつもりなので、是非統計の入門書としてご活用ください。

iBooksバージョン（Apple Books）




Kindleバージョン（Amazon）


2018/07/18

どれをインストールしたらいい？医療で使える統計解析ソフトウェア６選


SAS、JMP、SPSS、EZR（R）、Pythonなどの統計解析用のソフトウェアは有料から無料まで数多くあり、 どのソフトウェアが自分に一番合うか分かりません。EXCELから一歩進みたい方のために各ソフトの特徴をまとめました。

医療統計を学ぶための解析ソフトウェアの選択


統計の知識がついてくると、数式の結果をソフトウェアで確かめたくなります。 普段からEXCELでグラフ作成をしたり、平均や分散の他にも関数を使いこなしている方でも、本格的なデータ解析ができるソフトウェアに乗り換えるにはいくつかのハードルがあります。
  • そもそもどの統計解析ソフトウェアを使ったらいいかわからない
    統計ソフトには無料から有料のものまで数多くの種類があります。ソフトウェアにより、その使い方も異なります。例えば、データを選択するだけで済むものもあれば、プログラムを組む必要のあるものもあります。 
  • インストールが複雑かつ面倒
    手軽に統計ソフトウェアを試せない理由の１つとして、ソフトウェアのインストールがあります。EXCELではソフトを起動すれば合計や平均を関数で簡単に求めることができます。無料の統計解析ソフトウェアの中にはすぐに起動できずに、ソフトウェア本体をインストールするためにパッケージ管理ソフトやライブラリーを事前にインストールすることから始める必要がある場合があります。インストーラーをダウンロードして起動、次、次、OKというようにはならなくて、何をインストールするのかコマンドラインに打ち込む必要があるということです。統計ソフトを使って統計を学びたいのに、事前に何ができるのかを知っていないとインストールできないということが問題です。
    余談ですが、エクセルでも複雑なデータ処理を行うこともできますが、少し見えにくいところ（アドイン）から機能を追加するようになっています。 
  • もちろん使い方は統計解析ソフトウェアによりマチマチ
    元になる計算は一緒でも表記だけでなく文法を含めて書き方が違います。書店にいけば様々な統計ソフトに対応した書籍が並んでいますが、同じ内容の解説をしている部分を比較してみれば、使っているソフトによってプログラム例、結果の表示まで、実行例が違います。

どのような統計ソフトが有名か

統計のソフトには下記の5種類が知られています。どのソフトも様々なデータ形式に対応しているので、EXCELで学習したデータが無駄になることはないでしょう。特に、統計検定2級以上を受けようと思っている方などは実地にデータを入れて試してみたくなるのではないでしょうか。また、これらのソフトは決して高価なもしくは高機能な Excelではないです。統計処理するデータがAIや機械学習の分野にまで及んだ時点でEXCELで処理できるデータ数と操作が追いつかなくなります。

有料 
  • SAS
  • JMP
  • SPSS
    有料のものでも体験版やアカデミック版で試用感を確かめることができます。 
無料

SAS（Statistical Analysis System）


医療関係の第3相試験では申請時資料に使用するためにSASが用いられていることが多いように思います。 医師主導の臨床試験で行われた試験報告にはJMPやSPSS時にはExcelも出てくることがあります。高価である分だけ信頼性も高く解析の手法も多岐に渡ります。アカデミック版のSASがあるのでSASを使いこなせるのは理系で専門の教育を受けた人になるのではないかと思います。デザインの世界でAdobeのPhotoshopやillustratiorを使うような感覚だと思います。 

JMP

JMP (ジャンプ)はSASのJMPビジネスユニットにより開発されました。データの可視化とパワフルな統計機能をあわせ持ち、インメモリで処理を行うデスクトップ用ソフトウェアです。1989年当初にAppleのMacintosh用に作成されたものだけあって直感的な操作に適しています。2018年現在、３０日間の無料トライアルと年間ライセンス版、パッケージ版が提供されています。 

SPSS


SPSSは2009年にIBMが買収以降、統計解析ソフトウェアの製品群として提供されています。 予測分析ソフトウェアとして商用のパッケージになります。 

R言語（EZR）


1984年にAT&Tベル研究所で研究・開発された統計処理言語であるS言語を元にしたオープンソース・フリーソフトウェアです。様々なパッケージをインストールすること統計に適した解析環境が出来上がります。 マウス操作だけで解析できるRコマンダーのカスタマイズ機能を組み込んだソフトウェアがEZR (Easy R)です。特に生存解析、ROC曲線解析、メタアナリシス、サンプルサイズの計算など、医療統計で役立つ解析が充実しています。 


Python


Pythonの発案者はグイド・ヴァンロッサムで1990年代初頭から開発が行われています。 万人のためのコンピュータプログラミングを目指しており、オープンソースで平易であり、開発時間を短くできるような工夫をしています。Python本体は最小限の機能を提供し、統計処理や機械学習、AI、Webのフレームワークなどは別途必要なものをインストールして使用します。 
私は統計だけでなく、Webサービスとの連携も考慮した環境を得たかったのでPythonを使用しています。 Pythonで面食らうのは、バージョンとインデントです。バージョンの２.0と３.0でプログラムの記載方法が若干異なり、Webに掲載されているサンプルプログラムがそのまま動かないことがあります。例えば、print文のバージョン3.0では「（）」が必要になります。 他の言語ではインデントはプログラムの可読性をよくする意味で使いますが、pythonの場合はスペースの開け方を間違うとエラーが出ます。 
Pythonの生みの親として知られるグイド・ヴァンロッサムさんですがgoogleにいたこともあるようです。you tubeやらdropboxも実はpythonで書かれていたということがあります。 

SAS、JMP、SPSS、EZR、Python結局どれがいい？


SASやJMPなどの有料版が適しているのは、企業や大学などでライセンスがあり近くに聞ける人がいる状況がある場合です。お金に余裕がある個人とかもいいかもしれません。また、企業のトレーニングコースも参考になると思います。 統計検定や治験の統計解析に関わるのではなく、理解を深めるために統計解析の結果を試したいのであれば、R言語（EZR）やPythonが適しているように思います。EZRは論文での引用もされていますし、R言語はライブラリがかなり整備されています。Webとの相性はPythonの方がいいように思いますが、場合によってはライブラリーのバージョンを合わせる必要があったりと、細かな調整やある程度プログラムを組まないといけないことがあります。 ただ、いずれの言語にしても相互に乗り入れる仕組みがあるので1つのソフトをまずはじっくり使えるようになることがいいと思います。

2018/07/01

検定の種類が分かる書籍の紹介。医療文献での統計法の選択と理解。


他人の執筆した文献でグラフには検定法が記載されておらず、「statistical analysis」の項目に複数の検定法が列記されているのに困ったことはないでしょうか。単純な臨床試験ではどのように試験が行われているかが分かれば統計手法も選択できます。この選択肢は統計の選択図としてまとめられていることがあります。
ただ、母集団の推測やデータの尺度、検定と推定の考え方など基礎的な統計の概念が分かっていないと検定選択の図を利用することができません。

教科書的な手法ではこれらの統計で扱うデータについて考え方を整理した上で、統計を数式で解いて理解することになります。

今回紹介する書籍では統計処理に必要な数学的な部分をロボットとして関数で表すことで本来数式で説明するところを全部絵で解説しています。イラストはポップなイメージですが抽象的な難しい概念の理解として、ブラックボックスですむところを上手くカバーしています。統計の全体像を読み物として知りたい方にいいと思います。

某書店で研修医向けの書籍として平積みされていましたので書店でもオススメのようです。


ぜんぶ絵で見る医療統計〜身につく! 研究手法と分析力

（関連リンク）
医学書院／週刊医学界新聞(第2927号 2011年05月09日)

2018/06/30

pythonプログラミング入門（２）グラフでサブプロットを描画


いくつかのグラフを1つにまとめるにはsubplotを使用します。subplotをどのように使用したらいいのか分かりにくかったのでまとめました。

subplotのカッコ内の数字によりグラフのまとめ方が決まります。subplotの後のカッコ内に数字が3つ並びますが、最初が縦のグラフの個数、２番目が横のグラフの個数、最後がどのグラフを指しているかになります。



実際のコード例を示します。 subplotでグラフを指定した後に、データの設定やy軸名などのラベルの指定をします。

subplotのコード例

import matplotlib.pyplot as plt 

plt.figure(1)

plt.subplot(321)
plt.plot([1,2,3,4]) 
plt.ylabel('321') 

plt.subplot(322)
plt.plot([1,2,3,4], [1,4,9,16], 'ro') 
plt.ylabel('322') 

plt.subplot(323)
plt.plot([1,2,3,4], [1,4,9,16], 'bo') 
plt.ylabel('323') 

plt.subplot(324)
plt.plot([1,2,3,4], [1,4,9,16], 'yo') 
plt.ylabel('324') 

plt.subplot(325)
plt.plot([1,2,3,4], [1,4,9,16], 'go') 
plt.ylabel('325') 

plt.subplot(326)
plt.plot([1,2,3,4], [1,4,9,16], 'rx') 
plt.ylabel('326') 

#Matplotlib v1.1 introduces a newcommand tight_layout() that does this automatically for you.
#グラフが重なった時にレイアウトを自動的に調整してくれる。(後述)
plt.tight_layout()

plt.show()

subplotを使用した表示例



グラフの自動レイアウトについて（tight_layout()）

plt.tight_layout()はグラフのレイアウトを自動で調整するコマンドです。 コマンドを指定しないとy軸名がグラフと重なってしまいます。

plt.tight_layout()がない場合

（関連コンテンツ）
登録: 投稿 (Atom)